The Mathematical Reason You should have 9 Kids

In this post I propose a curious genetic question that can be modeled with a remarkably simple answer. If you have $ N $ children, what is the probability that every allele in your genome is present in at least one of your children? In other words, if you have $ N $ children, what is the probability that your entire genome has been replicated in the next generation?

Note: I do not believe there is a correct number of children to have. This blog post is just for fun. An organism's biological purpose is not to replicate its genome. Rather, an organism's biological purpose is simply to reproduce.
For an explanation of biological purpose, I invite you to read Debunking the Selfish Gene by T. K. Van Allen.

As a human, you have two sex chromosomes XY or XX, and you have 22 homologous pairs of autosomal chromosomes (autosomes) numbered 1 through 22. Your child receives 23 chromosomes from you and 23 chromosomes from the other parent. The manner in which each chromosome is transmitted to your child is independent of the manner in which the other chromosomes are transmitted to your child. Each autosome has a roughly $ \frac12 $ probability of being transmitted as a crossover of your own homologous autosome pair during cellular meiosis. And each autosome has a roughly $ \frac12 $ probability of being transmitted as an identical copy of 1 of your 2 corresponding homologs during cellular meiosis.

In this image, chromosomes of different size correspond to differently numbered chromosomes. Chromosomes of the same size and different single colors correspond to homologs of the same numbered chromosome. The H-shaped things are two chromatids attached at a centromere, and the 1-shaped things are lone chromatids. Dual-colored chromatids were generated by a crossover event during meiosis I. The end result of meiosis is 4 gamete cells. A single gamete cell from each of 2 parents fuse to form the zygote.
Source: Wikimedia Commons

Because chromosomes are transmitted independently, the probability that all of your autosome pairs are replicated into your children is just the probability that one of your autosome pairs is replicated into your children, raised to the power of 22.

Below, I derive a formula for the probability that an autosome pair is replicated into your children if you have $N \gt 0$ children.
The probability is given by: $$ 1 - \frac{N+2}{2^N} + \frac{1}{2^{2N-1}}.$$

Probability of genome replication for males

After a male has $N$ children, it is immediately apparent whether or not the X and Y sex chromosomes were both replicated into his children. So the probability that X and Y were replicated is determinate, either 0 or 1, not probabilistic. The probability that his full genome was replicated into $N$ children is given by the probability that each of 22 autosomes were replicated into $N$ children: $$ \left(1 - \frac{N+2}{2^N} + \frac{1}{2^{2N-1}}\right)^{22}. $$ Before a male has $N$ children, it is still probabilistic whether or not the X and Y sex chromosomes will be replicated into his children. The probability that both are replicated is given by $1-\left(\frac12\right)^{N-1}$ when $N \gt 0$. The probability that his full genome will be replicated is given by: $$ \left(1-\left(\frac12\right)^{N-1}\right)\left(1 - \frac{N+2}{2^N} + \frac{1}{2^{2N-1}}\right)^{22}.$$

Probability of genome replication for females

The female's XX chromosomes behave like autosomes during meiosis, where each gamete has a roughly $\frac12$ probability of receiving a copy homolog and a $\frac12$ probability of receiving a homologous pair crossover. So the probability that her full genome was replicated into $N$ children is given by the probability that each of 23 autosomes were replicated into $N$ children: $$ \left(1 - \frac{N+2}{2^N} + \frac{1}{2^{2N-1}}\right)^{23}. $$

Results

The results are summarized in the following graph:

In all cases, for an individual to have better-than-even odds at replicating his/her entire genome, s/he must have 9 children.

Suppose that a couple wants to consider the probability that both of their genomes are replicated into their shared children. To determine this probability, they just multiply their individual probabilities together. The results are summarized in the following graph:

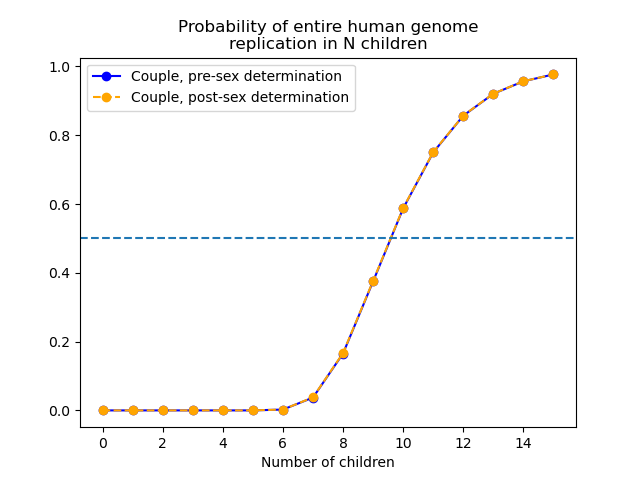
In both cases, for a couple to have better-than-even odds at replicating their genomes, they must have 10 shared children.

Calculating the probability that an autosome pair is replicated if you have $N \gt 0$ children:

We will calculate the probability that an autosome pair is replicated into your children by calculating the complement of the probability that an autosome pair is not replicated into your children.

Let us choose a particular autosome pair in your genome, and label it autosome pair $ A $. Let us give the label $ P $ to the homolog you received from your father (paternal), and let us give the label $ M $ to the homolog you received from your mother (maternal). If you have $ N\gt 0 $ children, there are 4 possibilities to consider:

Possibility 1: None of your children received a copy of the $ P $ homolog or a copy of the $ M $ homolog. They all received crossovers. This occurs with probability: $$ \left(\frac12\right)^N.$$
Possibility 2: None of your children received a copy of the $ M $ homolog, but $j \gt 0$ children received a copy of the $ P $ homolog. This occurs with probability: $$ {N \choose j} \left(\frac14\right)^0 \left(\frac14\right)^j \left(\frac24\right)^{N-j}\\ = {N \choose j} \left(\frac12\right)^{N+j}.$$
Possibility 3: None of your children received a copy of the $ P $ homolog, but $j \gt 0$ children received a copy of the $ M $ homolog. As above, this occurs with probability: $$ {N \choose j} \left(\frac12\right)^{N+j}.$$
Possibility 4: At least one child received a copy of the $ P $ homolog and at least one child received a copy of the $ M $ homolog. Then the probability that the autosome pair was not replicated into your children is $0$, so we can ignore this case.

Each crossover event occurs at a point along the length of the chromosome. The probability that two crossover events occur at the exact same location is $0$ (this is not exactly true, but it is virtually true). If there are $i$ number of $P$-$M$ crossovers for autosome pair $A$, out of $R$ total crossovers for autosome pair $A$ among your children, then there will be $R-i$ number of $M$-$P$ crossovers for autosome pair $A$ among your children.

Possibility 1

If you have $ N $ children and each receives a crossover of your autosome pair $ A $, then the following describes the criteria for which the full $ P $ homolog will not be replicated among your children:

If all the crossover sites for $P$-$M$ crossovers occur higher along the length of the chromosome than all the crossover sites for $M$-$P$ crossovers, then the full $P$ homolog will not be replicated.

Similarly, here is the criteria for which the full $M$ homolog will not be replicated among your children:

If all the crossover sites for $M$-$P$ crossovers occur higher along the length of the chromosome than all the crossover sites for $P$-$M$ crossovers, then the full $M$ homolog will not be replicated.

The ordering of crossover sites along the length of a chromosome can be represented by an $N$-length sequence of $p$s and $m$s, where $p$ represents a $P$-$M$ crossover and $m$ represents an $M$-$P$ crossover. There are $2^N$ possible sequences and they are all equally likely.

Sequences that are $i>0$ number of $m$s followed by $N-i$ number of $p$s fulfill the first criteria. There are $N$ such sequences. Sequences that are $i>0$ number of $p$s followed by $N-i$ number of $m$s fulfill the second criteria. There are $N$ such sequences. In total there are $2N$ sequences in which at least one homolog will not be replicated, out of $2^N$ equally likely sequences, so the probability that at least one homolog is not replicated is given by: $$ \frac{2N}{2^N} = \frac{N}{2^{N-1}}. $$

Together, the probability that none of your children received a copy homolog and that at least one homolog is not replicated by the crossovers is given by: $$\left(\frac12\right)^N\left(\frac{N}{2^{N-1}}\right) = \frac{N}{2^{2N-1}}.$$

Possibility 2

Suppose $j \gt 0$ children received a copy of the $P$ homolog and $0$ children received a copy of the $M$ homolog. Let $n$ be equal to $N-j$. Then the following describes the criteria for which the full $M$ homolog will not be replicated among your children:

The ordering of crossover sites along the length of a chromosome can be represented by an $n$-length sequence of $p$s and $m$s, where $p$ represents a $P$-$M$ crossover and $m$ represents an $M$-$P$ crossover. There are $2^n$ possible sequences and they are all equally likely.

Sequences that are $i \ge 0$ number of $p$s followed by $n-i$ number of $m$s fulfill the criteria. There are $n+1$ such sequences, out of $2^n$ equally likely sequences, so the probability that the $M$ homolog is not replicated is given by: $$ \frac{n+1}{2^n} = \frac{N-j+1}{2^{N-j}}. $$

Together, the probability that $j$ children received a copy of the $P$ homolog, $0$ children received a copy of the $M$ homolog, and the $M$ homolog was not replicated by the crossovers is given by the following: $$ {N \choose j}\left(\frac12\right)^{N+j} \left(\frac{N-j+1}{2^{N-j}}\right)\\ ={N \choose j} \frac{N-j+1}{2^{2N}}.$$

Summing over possible values of $j$ (see https://mathworld.wolfram.com/BinomialSums.html for formulae on weighted binomial sums), we have the total probability that at least $1$ child received a copy of the $P$ homolog, and $0$ children received a copy of the $M$ homolog, and the $M$ homolog was not replicated by crossovers: $$ \sum_{j=1}^N {N \choose j} \frac{N-j+1}{2^{2N}}\\ = \frac1{2^{2N}}\left[\left(N+1\right)\sum_{j=1}^N {N \choose j} - \sum_{j=1}^N j {N \choose j} \right]\\ = \frac1{2^{2N}}\left[\left(N+1\right)\left(2^N-1\right) - N2^{N-1}\right]\\ = \frac{N+2}{2^{N+1}} - \frac{N+1}{2^{2N}}.$$

Possibility 3

As above, the probability that at least $1$ child received a copy of the $M$ homolog, and $0$ children received a copy of the $P$ homolog, and the $P$ homolog was not replicated by crossovers is given by: $$\frac{N+2}{2^{N+1}} - \frac{N+1}{2^{2N}}.$$

Possibility 4

The probability that at least one child received a copy of the $P$ homolog, at least one child received a copy of the $M$ homolog, and either homolog is not replicated is $0$.

Combining Possibilities 1-4

If $N \gt 0$, the probability that autosome pair $A$ was not replicated into $N$ children is given by: $$ \frac{N}{2^{2N-1}} + 2\left[\frac{N+2}{2^{N+1}} - \frac{N+1}{2^{2N}}\right] \\ = \frac{N+2}{2^N} - \frac{1}{2^{2N-1}}. $$

If $N \gt 0$, the probability that autosome pair $A$ was replicated into $N$ children is given by: $$ 1 - \frac{N+2}{2^N} + \frac{1}{2^{2N-1}}. $$